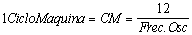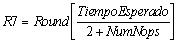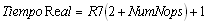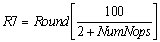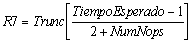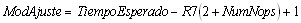Subrutinas de Tiempo

Salvador Macías Hernández

Página hecha el Lunes 01 de Mayo del 2006

INTRODUCCIÓN

A veces es necesario que el microprocesador espere cierto intervalo de tiempo, para realizar acciones. Ya sea que requiramos que nos prenda y apague un led cada dos segundos, o bien hagamos un pequeño semáforo, o estemos abriendo una válvula durante 15 minutos para regar el pasto, etc. Al finalizar el estudio podrás utilizar el Generador de Subrtonas de TIempo

DE LA FAMILIA MCS51 DE INTEL

Recordemos que en la familia de microcontroladores Mcs51 de Intel. El ciclo de Máquina está dado por 12 veces el ciclo de reloj.

 Por ejemplo: Si el cristal de cuarzo que se está utilizando es de 12Mhz, el ciclo de máquina será de 1mS; Si el cristal ahora es de 4Mhz, el ciclo de máquina será de 3mS.

Hay que tener en cuenta, que cada instrucción que ejecuta el microcontrolador, le lleva cierto tiempo, o ciertos ciclos de máquina. Generalmente las instrucciones utilizan de uno a dos ciclos de máquina, pero hay instrucciones que consumen más ciclos de reloj. Para saber cuantos ciclos de reloj (periódos de oscilador) consume  cada instrucción, debes consultar el documento MCS-51 Programmer's Guide and Instruction Set. Así por ejemplo la instrucción NOP, consume un ciclo de máquina o 12 ciclos de reloj. A continuación vemos una tabla con las instrucciónes más utilizadas para hacer subrutinas de tiempo:

SUBRUTINAS DE TIEMPO SIMPLES

Entonces, por ejemplo:

El siguiente segmento de programa consume 3 Ciclos de Máquina, o lo que es lo mismo 36 ciclos de reloj. Si suponemos que el cristal es de 12 Mhz. El segmento de este programa consumiría 3*(12/12Mhz) = 3 micro segundos.

Ahora bien, que pasaría si quisiéramos hacer una subrutina que consumiera 50mS, necesitaríamos poner 50 NOP's. O bien si en vez de 50mS requiriéramos 1mS, entonces necesitaríamos poner 1000 NOP's. Lo cual es totalmente inviable. Por eso aplicamos bucles para repetir unos cuantos NOP's un determinado número de veces.

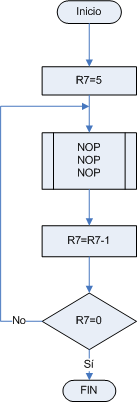
Analicemos el siguiente programa:

El programa comienza asignando el valor de 5 decimal al registro siete. Enseguida deja pasar tres ciclos de máquina (por los tres siguientes NOP) y después decrementa el registro siete (ya no va a valer 5, ahora va a valer 4), y compara si el nuevo valor de R7 (4 decimal) es igual a cero, si es igual a cero salta a la siguiente línea (fin de nuestro programita) y si no es cero, salta a la etiqueta PrimerCiclo. En este caso como el valor de R7 es 4 y no es igual a cero, el microcontrolador saltará a la etiqueta PrimerCiclo. Y una vez allí volverá a dejar pasar 3 ciclos de máquina (por los 3 NOP) y volverá a decrementar y a comparar, y como tampoco va a ser cero (por que R7 valdría 3), volverá a saltar a la etiqueta PrimerCiclo. Todo este proceso se llevará a cabo 5 veces, que es cuando R7 valdrá cero. Y para fines de nuestra subrutina de tiempo, esto nos significa que vamos a multiplicar 5 veces el tiempo de las instrucciones que se encuentran dentro del ciclo. 

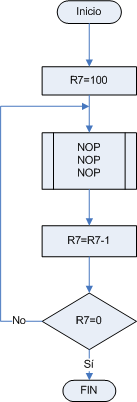
Y si cambiásemos la primera instrucción, para que en vez de que cargue 5 en R7, cargue 100, entonces estaríamos multiplicando todo lo que hay dentro del ciclo por 100, lo que nos consumiría 501 ciclos de máquina, o 501 ms.

ESTRUCTURA DE SUBRUTINAS DE TIEMPO SIMPLES CON BUCLE SIMPLE

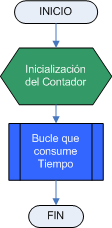
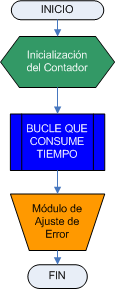
La estructura de las subrutinas de tiempo simple con bucle simple es la que se muestra en el siguiente diagrama:

Del programa anterior vamos a indicar el con color verde la instrucción de Inicialización del Contador, y con color azul las instrucciones del Bucle que consume Tiempo.

Como se puede apreciar, la parte medular de la subrutina es la del Bucle puesto que es la parte que más consume tiempo. Para el caso del anterior programa se muestra una tabla con los tiempos que aporta cada parte de la subrutina, expresado en microsegundos y también se indica el porcentaje que aporta.

DISEÑO DE SUBRUTINAS DE TIEMPO SIMPLES CON BUCLE SIMPLE

Para hacer una subrutina que consuma un tiempo determinado, hay que realizar los siguientes cálculos:

   Dónde:

               CM= Ciclo de Máquina y está dando en microsegundos

               Frec.Osc= Frecuencia del Oscilador (cristal de cuarzo) y está dado en Mega Hertz

   Dónde:

               R7= Es el valor del Registro Siete, éste valor tiene que ser entero

               TiempoEsperado= Es el tiempo que debe de consumir nuestra subrutina, en microsegundos

               NumNops= Es el número de instrucciones NOP que tendrá el bucle

   Dónde:

               TiempoReal= Es el tiempo que la subrutina va a consumir en la realidad

               TiempoEsperado= Es el tiempo que debe de consumir nuestra subrutina, en microsegundos

               NumNops= Es el número de instrucciones NOP que tendrá el bucle

Ejemplo:

      Se desea diseñar una subrutina simple de bucle simple que consuma 100 microsegundos, en un microcontrolador de la familia MCS51 y que tiene un cuarzo de 12Mhz

Frec.Osc=12;                       TiempoEsperado=100

Usando las Fórmulas anteriores se deduce que:

CM= 1

Si elegimos arbitrariamente el valor de NumNops igual a 1, tenemos:

R7 = 33

Entonces el programa quedaría así:

Hay que fijarnos que R7 siempre debe de ser entero, por eso se aplica la función Round, que lo que hace es redondear el resultado de la división al número entero más próximo, es decir: si la división te da 32.8, hay que redondearlo a 33 y si te da 32.2 hay que redondearlo a 32. Al hacer ese redondeo, generamos un error, que es la diferencia entre el TiempoReal y el TiempoEsperado

Error = TiempoReal - TiempoEsperado

Para este caso en particular tenemos que el error es cero.

TiempoReal=R7(2+NumNops)+1= 33 (2 + 1) +1= 100

Error= 100 - 100 = 0

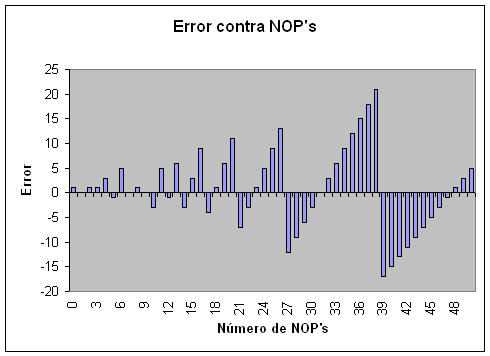
Cuando nuestro error es cero, como en este caso, se dice que tenemos una solución ideal. Cuando el error es el mínimo, se dice que tenemos la solución óptima. Para conseguir la solución ideal o la óptima, es necesario hacer estos cálculos con diferentes valores para ver cual es el que requerimos. Para hacer más simple este proceso, se hizo una hoja de calculo en Microsoft Excell  2003: SubTimeBucleSimple.xls en el cual solo tienes que ingresar el valor del cristal (Frecuencia del Oscilador) y el Tiempo Requerido, y automáticamente te saldrá una tabla con los valores de Número de NOP's y el Valor de R7, así como la Gráfica de Valores y de Error

Imagen de la Hoja de Excel SubTimeBucleSimple.xls

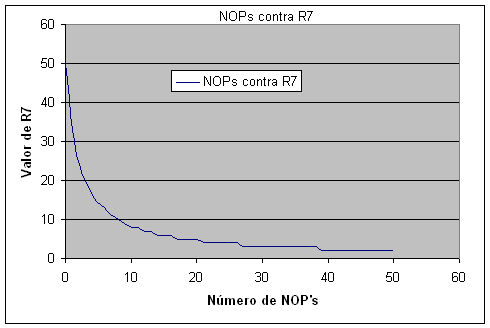
Gráfica de R7 contra el Número de NOP que debe tener el bucle

Grafica del Error contra el Número de NOP que deberá tener el bucle

SUBRUTINAS DE TIEMPO COMPLEJA CON BUCLE SIMPLE

      Como podemos ver las subrutinas de tiempo pueden tener un error implícito, una manera de reducir ese error es insertar un módulo de ajuste, que es una serie de NOP al final de la subrutina simple (formando una subrutina compleja), de forma tal que consuman el error. La estructura de la subrutina queda:

Para este tipo de subrutina, el valor de R7 se define como:

Donde la función Trunc, es la función truncar que no redondea el cociente, sino que únicamente toma el valor entero del mismo. Es decir, si es el cociente es: 33.89 la función resulta en: 33, si el cociente es: 33.2 la función resulta en: 33.

Para calcular el número de NOP's que integrarán el Módulo de Ajuste de Error se utiliza la siguiente fórmula:

Para calcular el Tiempo Real que consumirá esta subrutina, hay que usar la siguiente identidad:

Por ejemplo:

  Si deseamos hacer una subrutina de tiempo de 150uS y con 5 NOP's, el valor de R7 sería:

R7 = 21

El número de NOP's que integrarán el módulo de ajuste es:

ModAjuste = 150-21(2+5)+1= 2

Entonces la subrutina quedaría de la siguiente manera:

El tiempo real que consume esta subrutina sería:

TiempoReal=R7(2+NumNops)+ModAjuste+1= 150 CM

Como podemos ver, el tiempo real y el tiempo esperado es el mismo, ya que se ajustó con el último módulo, por lo que ya no es necesario calcular el error. Al igual que la subrutina anterior, se elaboró una hoja de Excel para obtener los valores mucho más rápidos: SubTimeComplBucleSimple.xls

Ahora bien una desventaja del método que acabamos de aprender es que tiene un máximo de tiempo, que es cuando R7 vale 255.No podremos hacer una subrutina de tiempo que dure una hora con esta metodología. Es por esto que surgen las subrutinas de bucle anidado.

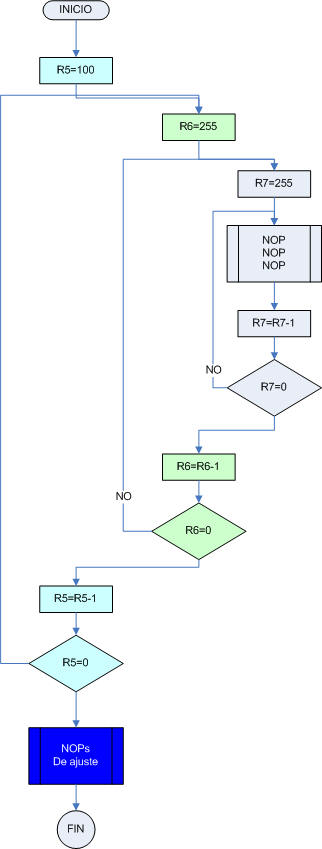
SUBRUTINAS DE TIEMPO COMPLEJA CON BUCLE ANIDADO

Las subrutinas de bucle anidado, lo que hace es meter un bucle dentro de otro,  en el diagrama de flujo que se muestra a continuación, tenemos tres bucles anidados, estos tres bucles anidados lo que hacen es multiplicar el tiempo que consume el bucle interior (R7). Por lo que con esta estrategia podemos hacer una subrutina de tiempo tan grande como deseemos

Generador de Subrutinas de tiempo

Bibliografía